2022年11月24日
個人で自社製品RISC-V CPUを買うことはできるか?その3 - 個人向け販売チャネル開設
目次: RISC-V
結論を先に言うと「面倒くさいけど個人でも買える」です。
Akaria NS31AのEntry Kitのご担当の方と何度かメールをやり取りしていただけで、あっというまに1週間経ちました。この時間があれば、中国や台湾のボードなら注文、支払いは全て終わって、家に届いていますね。さておき個人がNS31A Entry Kitを購入する場合の条件は下記の通りでした。
- 個人→担当: QAフォームから連絡(Webサイトは準備中とのこと)
- 個人→担当: 住所/電話番号を伝える
- 担当→個人: 見積書が送られてくる
- 個人: 萩原エレクトロニクス社の指定口座へ手数料負担で先払い
- 担当→個人: 注文書PDFが送られてくる
- 個人→担当: 注文書を印刷、捺印、スキャンして画像を返送
- 商品は「着払い」で届く
最近の便利な通販サービスに慣れきってしまったため、かなり面倒くさいのと、そんなことするの?という驚きでいっぱいです。Amazonや楽天がいかに簡単で素晴らしいかわかります。
通販らしくない
B2Bのみの販売経路に、個人への販売経路を追加していただいたのは感謝していますが、企業→個人で「着払い」で物が送られるのは初めてで驚きました。
通常は請求料金に送料を乗せます。3万円のボードなら送料を企業側が負担することも珍しくありません。個人でやっているレベルの小規模小売店もできていることです。払う総額は同じでも、個人側の負担を減らそう、料金を明瞭にしよう、という意気込みが欲しかった……。
企業が着払いを使うのは逆(個人→企業)の方向に送るときです。つまり個人側が送料を負担しなくていいように、企業が着払いで受け取ります。修理時の発送では割と見かけますね。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2022年11月16日
個人で自社製品RISC-V CPUを買うことはできるか?その2 - 個人向け販売チャネル検討中
目次: RISC-V
先日(2022年11月12日の日記参照)送ったNS31Aの評価キット購入についての問い合わせの返事が来ました。あまりに返事が来なくて、メールアドレス書き間違ったかな?って不安だったので安心しました。ちなみに返事の内容は、
- 個人向け販売は想定外だった
- 個人向け販売もできないか社内調整する
- 販売可能か不可能か今は答えられない
とのことです。QAフォームを見た時点で、これBtoB販売しか想定してないでしょ!?とは薄々感じていたので、やっぱりか〜と思いました。
というわけで、何かしらの決定&判断をいただけるまでもう少し待ってみます。
メモ: 技術系の話はFacebookから転記しておくことにした。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2022年11月14日
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2022年11月12日
個人で自社製品RISC-V CPUを買うことはできるか?その1 - 問い合わせ
目次: RISC-V
個人で自社製品を買おうとしたらどうすれば良いか?を調べました。NSITEXEのIPで世の中に出ているものは2種類ありますが、Akaria NS31Aという汎用RISC-V 32bit CPU IPを購入します。
CPU IPそのもの(Verilogのコード)を買うのはライセンス契約等が必要で個人ではほぼ不可能なので、CPU IPを試せるFPGAの購入を検討します。
とにかく買い方がわからなくて辛い
萩原エレクトロニクスがパートナー企業として評価キットを販売してくれています。しかしNSITEXE NS31Aで検索してもかなり下に評価キットのニュースリリースが出るのみで、製品紹介サイトはありません(NSITEXE製RISC-Vコア評価キット発売について - 萩原電気ホールディングス株式会社)。ニュースリリースですといずれ消えるのでは?大丈夫か……?
ニュースリリースにはAkaria NS31AのEntry Kitの特徴は「発売中」と書いてあるものの、買い方が一切書いていません。この時点で興味のあるエンジニアの3割が脱落すると思います。
めげずに読み進めて下の方にある「NSITEXE製RISC-Vコア評価キット製品紹介」というボタンを押すと、チラシがPDFで出てきます。Interface誌にもこのチラシが載っていました(チラシへのリンク)。
チラシを見ても相変わらず買い方がわからないです。あとQRコードだけという仕様も辛いです。PCユーザーを見捨てないでほしいです。この時点で興味のあるエンジニアの6割が興味を失って脱落すると思います。
すぐに買えないのはなぜ?
めげずにスマホを持ってきてQRコードを読むと、良くわからんQAフォームに飛ばされます(お問い合わせ - 萩原エレクトロニクス)。
出た出た!日本の半導体会社の最大の悪癖「営業にご連絡ください」攻撃です。この時点で興味のあるエンジニアの9割が脱落します。上司に言われて仕事で渋々買う人以外は連絡しませんよ。これ。
QAフォームを見ると会社名が必須で「個人の開発者など用はない、去れ」という気持ちがビシビシ伝わりますが、めげずに「個人ですが何か?」とフォームを埋めてメッセージを送信しました。
しばし待ってみましたが、特に確認メールなどは来ないようです。正常に送れたんでしょうか?不安になりますね。今日はいったんここまでです。買い方がわかったらまた続きを書こうと思います。
他国と比べてしまう
中国や台湾のメーカーはボード1つでも売ってくれるし、一瞬で注文できるし海を越えても届けてくれるのに、日本のボードは1日で発注にすら至らないし、すごく面倒くさいです。相当の機会損失していると思います……。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2022年11月11日
手動の最適化 対 コンパイラの最適化
ポッキーの日だそうですが、1(と0)といえば2進数、2進数といえばビット操作ですね(?)。以前 Bit Twiddling Hacks を最新のコンパイラ達に向けて試したときの悲しい結果をメモしておきたいと思います。
試したのはConditionally set or clear bits without branchingという項目で、fがtrueならwとmのビット論理和を、fがfalseならwからmのビットを消去した値を返す処理です。素朴な実装ではif文を使うでしょう。
1つ目の方式: Conditionally set or clear bits
int cond_set_or_clear1(bool f, int m, int w)
{
if (f)
return w | m;
else
return w & ~m;
}
さきほどのサイトでは最適化版として、条件分岐をなくす、データ依存性をなくす(スーパースカラプロセッサ用)、2つのバージョンを掲げています。まずは条件分岐をなくした版のコードを紹介します。
2つ目の方式: Conditionally set or clear bits (without branching)
int cond_set_or_clear2(bool f, int m, int w)
{
return w ^ ((-f ^ w) & m);
}
分岐がなくなっています。なんでこれで同じ動作をするのか?は説明が必要でしょう。fがtrueなら -f = -1となり、-f ^ wはwのビット反転(notと同じ)と同じ結果 -1 ^ w = ~wになります。よって右側の括弧内 (-f ^ w) & m = ~w & mです。
あとは~w & mはw = 0, m = 1のビットだけ1になって残り、あとは全部0になります。w ^ (~w & m) はw | mと同じ結果ですが……そう言われてもわかりにくいので表にします。
| w | ~w | m | ~w & m | w ^ (~w & m) |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
一方fがfalseの場合、0とみなされるので -f = 0となって、-f ^ w = 0 ^ w = wです。右側の括弧内 (-f ^ w) & m = w & mです。w ^ (w & m) は先ほどとは逆でw = 1, m = 1のビットだけ1になって残り、あとは全部0になります。
最後にwとこの結果をxorすることでwとmがともに1のビットだけ0になりますから、w ^ (w & m) はw & ~mと同じ結果です、が……これも表がわかりやすいでしょう。
| w | m | w & m | w ^ (w & m) |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 |
次にスーパースカラ版のコードを紹介します。
3つ目の方式: Conditionally set or clear bits (without branching, superscaler)
int cond_set_or_clear3(bool f, int m, int w)
{
return (w & ~m) | (-f & m);
}
これは先ほどよりシンプルです。左側の括弧はfによらず常にw & ~mで一定で、右側の括弧の値だけが変化します。
まずfがtrueなら -f = -1となり、-f & m = mです。(w & ~m) | mですが、w & ~mはwからmの1となっているビット位置を0にする演算でした。そこにmをorすると消えたビットは再び1になります。すなわちw | mと同じ結果です。
| w | m | w & ~m | (w & ~m) | m |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
次にfがfalseなら -f = 0となり、-f & m = 0です。よって (w & ~m) | 0 = w & ~mになります。
なぜスーパースカラ向けか書いていませんが、w & ~mと -f & mに依存性がなくて同時に演算できるからだと思われます。じゃあ全部これでいいじゃないか?と思われるかもしれませんが、演算回数を見ると、
2つ目の方式と3つ目の方式の演算回数
2つ目の方式: w ^ ((-f ^ w) & m) neg, xor, and, xorの4回の演算が必要 3つ目の方式: (w & ~m) | (-f & m) not, and, neg, and, orの5回の演算が必要
このため同時に演算できないプロセッサの場合は2つ目の方式の方が良いと言えます。
全てを無にするコンパイラの最適化
ここまで長々と紹介しておいてこんなことを言うのは憚られますけど。この手のビット魔術は面白いのでつい手を出したくなりますが、最近のコンパイラに対しC言語レベルでの最適化はあまり意味がないです。
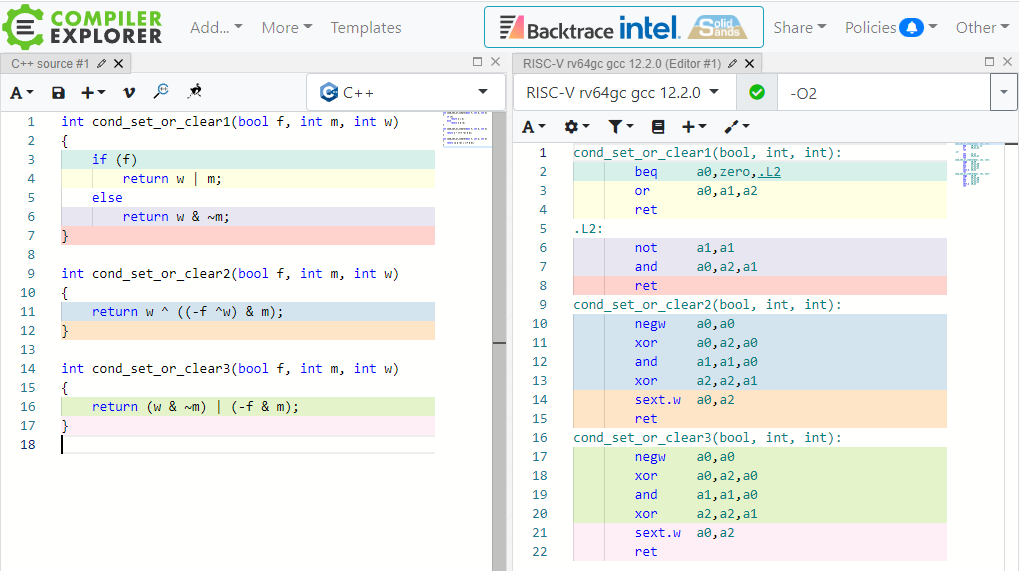
論より証拠でGCC 12.2.0の結果から見てみましょう。
あれだけグダグダ語った3つ目の方式でしたが、なんと2つ目の方式と全く同じバイナリになりました。
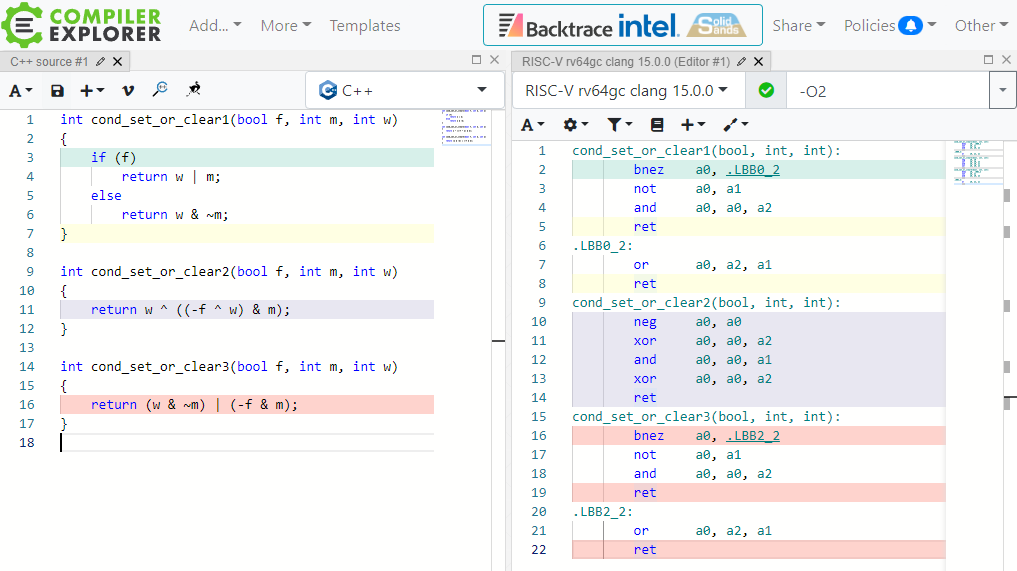
GCCだけでは証拠として不安でしょうか?では次にclang 15.0.0の結果も見ましょう。
なんと3つ目の方式は「これ分岐じゃね?」と解釈されて分岐に戻されてしまいました。これが分岐に見えるclangはスゴイですね。私はこのコードを見ても分岐には見えません……。
1つ目の方式と2つ目の方式が違うバイナリになるところを見る限り、全くの無意味ではないです。しかし見やすさでは大幅に劣ります。基本は素朴なコードにしておき、遅くて困る場合のみビット魔術に手を出すべきでしょう。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
| < | 2022 | > | ||||
| << | < | 11 | > | >> | ||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| - | - | 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | - | - | - |
最近のコメント5件
最近の記事20件
-
 26年2月11日
26年2月11日
すずき (02/14 13:38)
「[shebangの役割 - シェル側] 目次: Linux前回(2026年1月29日の日記参照)、スクリプトの先頭(例えばシェ...」 -
 23年4月10日
23年4月10日
すずき (02/14 03:04)
「[Linux - まとめリンク] 目次: Linuxカーネル、ドライバ関連。Linux kernel 2.4 for ARMが...」 -
 23年5月15日
23年5月15日
すずき (02/09 22:27)
「[車 - まとめリンク] 目次: 車三菱 FTO GPX '95の話。群馬県へのドライブ1群馬県へのドライブ2将来車を買い替え...」 -
 26年2月8日
26年2月8日
すずき (02/09 22:27)
「[車の修理……のはずが雪] 目次: 車以前(2025年11月21日の日記参照)、ジャガーさんの左前...」 -
 26年2月9日
26年2月9日
すずき (02/09 22:10)
「[SSLに対応 - Let's Encrypt] 目次: 自宅サーバー一昨年(2024年2月2日の日記参照)にJPRSドメイン...」 -
 23年6月1日
23年6月1日
すずき (02/09 22:09)
「[自宅サーバー - まとめリンク] 目次: 自宅サーバーこの日記システム、Wikiの話。カウンターをPerlからPHPに移植日...」 -
 24年2月2日
24年2月2日
すずき (02/09 22:09)
「[SSLに対応 - JPRSドメイン認証型SSL] 目次: 自宅サーバー今更感がありますが、このサイトもSSL対応にしました。...」 -
 26年2月1日
26年2月1日
すずき (02/02 23:17)
「[エンジン出力特性は三者三様] 目次: 車Automobile Catalogue(リンク)という素敵なサイトがありまして、各...」 -
 21年5月7日
21年5月7日
すずき (02/02 19:31)
「[LLVM - まとめリンク] 目次: LLVM一覧が欲しくなったので作りました。LLVMの本を買ったClangのmain関数...」 -
 26年1月19日
26年1月19日
すずき (02/02 19:31)
「[LLVMインストール] 目次: LLVMLLVMの公式サイト(リンク)にある手順そのものなんですけど、いつもググっていて面倒...」 -
 26年1月29日
26年1月29日
すずき (02/02 19:22)
「[shebangの役割 - カーネル側] 目次: Linux前回(2026年1月23日の日記参照)はshebang(ファイル先...」 -
 26年1月23日
26年1月23日
すずき (01/27 02:47)
「[shebangの役割] 目次: Linuxスクリプトの先頭(例えばシェルスクリプトなど)に書く"#!〜"から始まるおまじない...」 -
 26年1月21日
26年1月21日
すずき (01/22 02:55)
「[日本のテレビメーカーの衰退] ソニーがテレビ事業を分離するニュース(ソニーはなぜ、テレビ事業を「分離」するのか - 中国TC...」 -
 25年12月26日
25年12月26日
すずき (12/30 14:01)
「[Linuxのjournal操作メモ] 目次: Linux最近のLinuxディストリビューションはsystemdを採用している...」 -
 25年12月22日
25年12月22日
すずき (12/28 23:39)
「[ゲームを買ったら遊びましょう3] 目次: ゲーム前回の振り返り(2024年10月20日の日記参照)から1年経ちました。所持し...」 -
 21年12月28日
21年12月28日
すずき (12/25 00:40)
「[ゲーム - まとめリンク] 目次: ゲームNintendo DSを買ったパネルでポンDS最近の朝はパネポンDS聖剣伝説DSチ...」 -
 08年3月25日
08年3月25日
すずき (12/24 22:16)
「[シムシティDS2クリア] 目次: ゲームシムシティDS2のチャレンジモード「現代 温暖化」編をクリアして、スタッフロールを拝...」 -
 25年12月10日
25年12月10日
すずき (12/24 01:02)
「[LinuxからBIOS/UEFIの設定を取得する] 目次: Linux設定によって何か動作を変えたい、PC再起動するのが嫌な...」 -
 25年12月16日
25年12月16日
すずき (12/24 00:47)
「[initramfsの更新方法] 目次: Linuxいつも忘れてググっている気がするのでメモしておきます。Linuxカーネルを...」 -
 16年3月2日
16年3月2日
すずき (12/24 00:37)
「[Device Treeの謎] 目次: LinuxDevice Treeを使ってARM Linuxを起動したとき、どうやってコ...」
こんてんつ
 wiki
wiki Linux JM
Linux JM Java API
Java API過去の日記
 2002年
2002年 2003年
2003年 2004年
2004年 2005年
2005年 2006年
2006年 2007年
2007年 2008年
2008年 2009年
2009年 2010年
2010年 2011年
2011年 2012年
2012年 2013年
2013年 2014年
2014年 2015年
2015年 2016年
2016年 2017年
2017年 2018年
2018年 2019年
2019年 2020年
2020年 2021年
2021年 2022年
2022年 2023年
2023年 2024年
2024年 2025年
2025年 2026年
2026年 過去日記について
過去日記についてその他の情報
 アクセス統計
アクセス統計 サーバ一覧
サーバ一覧 サイトの情報
サイトの情報合計:
本日: