2021年2月28日
JIS配列キーボードとOADG配列キーボード
目次: PC
今まで、いわゆる日本語配列のキー配列のことを漠然とJIS配列と呼んでいましたが、どうもこれは正確ではないようです。
技術者たるもの、規格を粗末に扱ってはいけませんよね??
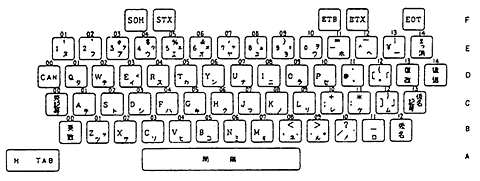
JIS配列を定めているのはJIS X 6002-1980「情報処理系けん盤配列」です。この配列を見ると一目瞭然ですが、アルファベット、スペースなどは一致するものの、他のキーは全く違う位置にあったり、そもそもなかったりします。規格書は有料(1,100円)ですが、PFUのサイトでJIS配列の図をタダで拝めます。
PFUのサイトへのリンク:
https://www.pfu.fujitsu.com/hhkeyboard/pfutechreview/section3.html
現状、主流の日本語キー配列はOADG(The PC Open Architecture Developers Group)が規格化した配列です。OADGは2004年に解散していますが、規格書はInternet Archiveで見ることができます。
Internet Archive: OADGテクニカル・リファレンス ハードウェア編1991年へのリンク:
https://archive.org/details/OADG1991/
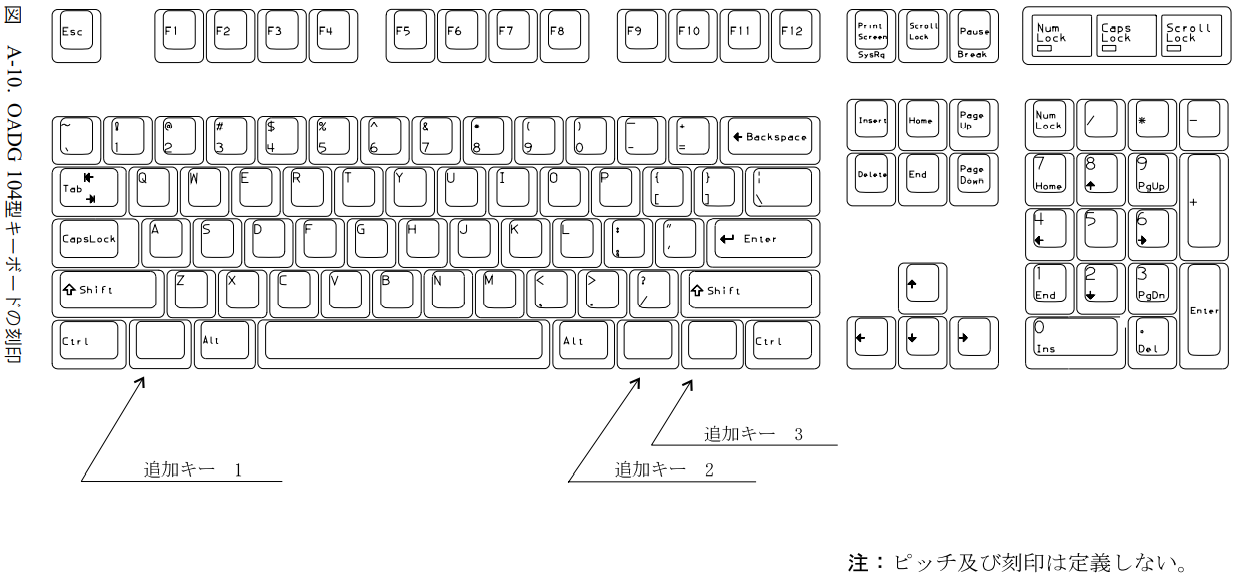
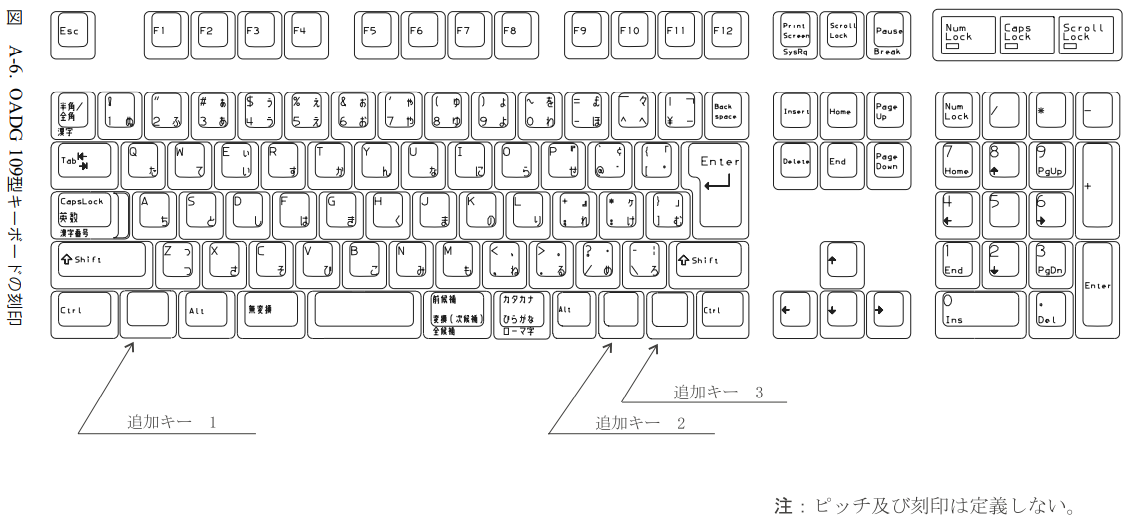
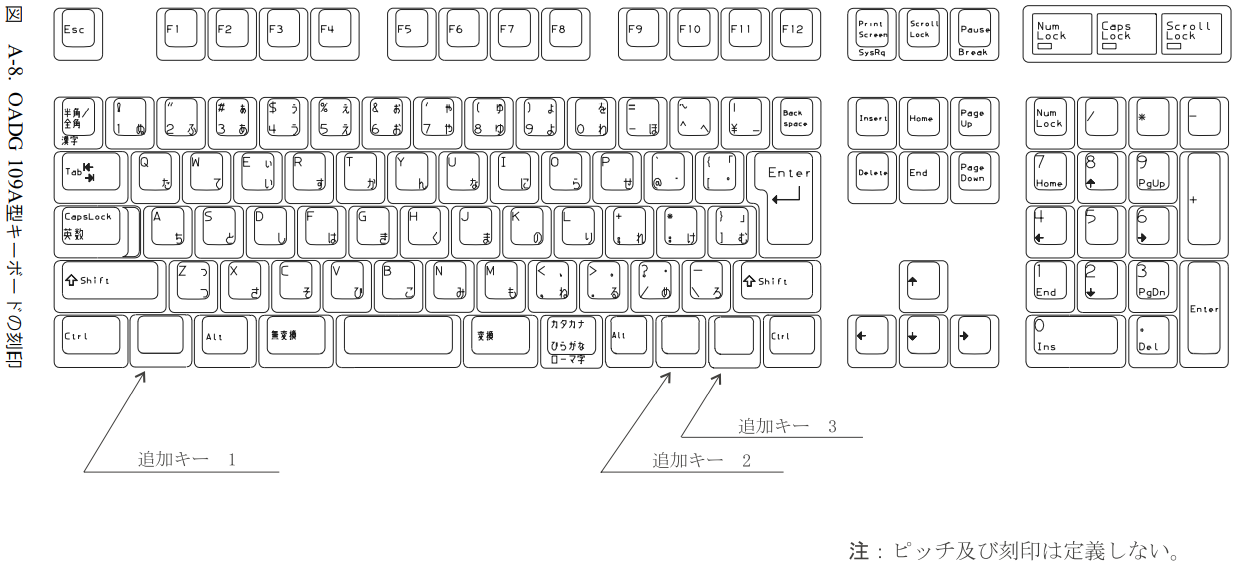
規格の付録Aを見ると、
- OADG 104型(英語配列)
- OADG 109型(日本語配列)
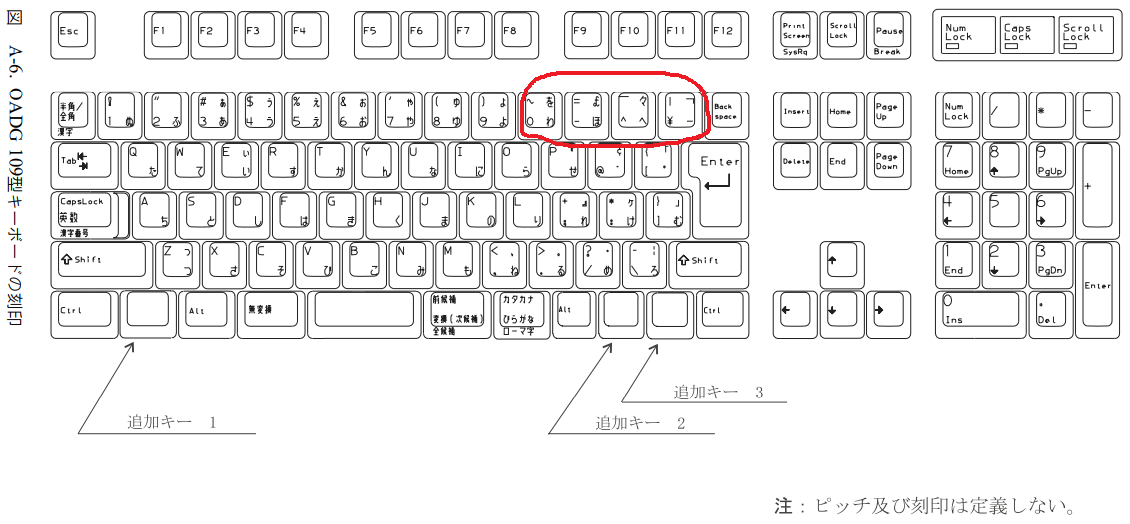
- OADG 109A型(109型と同じだが、- や ^ キーの刻印が違う)
の3つが書かれています。市販のキーボードは、各社ともに適当に魔改造しているため、OADG規格と全く同じキー配列のキーボードは存在しないと思います。たぶん。
実例を出すと、Logicool K295はかなり109Aに近いです。しかし、右Windowsキーが欠けています(このタイプ、俗に108キーなどと呼ばれていますね)。
FILCO Majestouchも素直な109Aに近いですが、右Appキーがなく、右WindowsキーがFnキーに置換されています。

FILCO Majestouch Convertible 2のキー配列
私の場合は、最下段は 左Ctrl, 左Win, 左Alt, スペース, 右Alt, 右Ctrlしか使わないので、K295やMajestouchのように使わないキーが欠けていても気になりませんが、使う人からすると、何てことするの!?という気分になるでしょう。
さらに言うと、無変換、変換、ひらがなキーも使わないので、使っているキーの種類だけ考えたら、いわゆる英語配列(OADG 104型)で十分に思えます。しかし日本語配列で練習したため、英語配列は記号類を間違えまくります。私物で購入したことはありません。打てて損はないので、もうちょい修行しても良いかもしれませんね……?
メモ: 技術系の話はFacebookから転記しておくことにした。写真追加、加筆。
コメント一覧
- hdkさん(2021/03/05 21:43)
109と109Aって、かなの記号も違うんですよ。"P"のあたりにある"『""』"なんかがなくなっていますよね。勝手な想像では、主流のWindowsで入力できないから消しちゃったんだと思いますが... ThinkPadでいうとX20とX30のところで違いが見られるようです。
OADG誕生前のIBM JXではこのへんの記号も入力できていましたし、\と¥や〜と ̄が刻印どおりに区別されていました。(なおJXは英文モード対応の関係なのか、英語部分はUS配列だったので、位置が違いますが。) - すずきさん(2021/03/06 00:21)
ですね、その辺りも違います。違いを全部示すつもりはなかった(本文と関係ないし)のですが、下手に赤丸で囲ったのが良くなかったか……。
 この記事にコメントする
この記事にコメントする
2021年2月27日
新キーボードMajestouch購入
目次: PC
先日の在宅勤務環境改善(2021年2月12日の日記参照)にて、デュアルディスプレイにしたところ、ノートPC本体が邪魔になってしまったので、机の上からどけました。
当然、ThinkPad本体のキーボードには手が届きませんから、ワイヤレスキーボードLogicool K295を買いました。Amazonで1,900円くらいでした。K295は変なキーも少ないし、静かで良いですが、キーの認識が渋いです。私の場合、打鍵力が足りず人差し指担当のキー(T, Uなど)の誤打が多発してイライラします。
買ってすぐ買い替えるのもどうかと悩みましたけど、あまりに誤打が多く慣れるまで辛そうだったので、さっさと諦めFILCOのMajestouch赤軸を買いました。ヨドバシで15,000円くらいでした。Majestouchはキーが戻るとき&底打ちしたとき「カーン!」と響く鐘のような音がやかましい以外は、非常に良いキーボードです。
キーボード使用歴
今まで、キーボードは標準的なキーボード(※)であれば、高くても安くても使い心地が気になることはないと思っていました。しかし今回K295がどうも合わなかったことから、実は自分とキーボードの相性って結構あるのか?と疑問に感じるようになりました。
(※)OADG 109A型の配列で、カーソルキー、ファンクションキー等の位置を移動していないキーボードのこと。
まずはキーボードの使用履歴を書き出してみます。
相性とか全く気にならなかった。
- DELLの標準キーボード
- Gatewayの標準キーボード
- HPの標準キーボード
- IBM/Lenovo ThinkPad X, Eシリーズ
- Logicool K270
- Majestouch赤軸
- NEC VersaPro
- Owltechの安いキーボード
- RealForce 108UBK
- サンワサプライの安いキーボード
- SONY VAIO Type-G
- TOSHIBA Dynabook R73
誤打しやすかった。
- Let's Noteシリーズ(理由: キーの形が横長)
- Logicool K295(理由: キーの認識が渋い)
- Logicool K340(理由: カーソル、ファンクションキー配置が変)
まともに打てなかった。
- HappyHacking(理由: キー配置が変すぎる)
以前K340やHHKで懲りて、特殊なキー配列のキーボードに触らなくなったので、コンパクト系のキーボードの利用歴はほぼゼロです。そもそもまともに打てないし、レビューできません。
ほとんどPC付属キーボード、ノートPCのキーボードばかりです。これはもしや、勝手に安物だと思いこんでいたPC付属の標準キーボード、実は質が高かったのではなかろうか?
大事な製品に標準で付属するものですし、高級ではないにせよ、あまりに変なものはつけませんよね。これが答えなのでは、という気がしてきました。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月25日
Slideshare初利用
Slideshareを初めて使いました。LinkedInのアカウントが必要なのは知りませんでした。偶然LinkedInのアカウントを持っていたので、すんなり登録できました。
USB PDはもっとわかりやすくしてほしい
試しに USB Type-C, USB PDケーブルとお友達になろうをアップロードしました。ダウンロードもできるし、スライド置き場として優秀ですね。みんな使うわけだ……。
スライドの話もしておくと、USB Type-Cケーブルがどうして何種類もあって、値段が全然違うのか、気になったので調べたことをまとめたものです。USB初心者なので間違ってたらすみません。
最後まで分からなかったのはUSB Power Deliveryの3A/5Aケーブルを見分ける方法です。何か無いんでしょうか。当然USB PDのアナライザで見ればわかりますよ?でもアナライザなんか普通の人は持ってませんよ。パッケージから出した途端に見分けが付かなくなるなんて、一般消費者からしてみたら辛すぎません?
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月16日
一般のご家庭にPCは何台ある?
目次: PC
内閣府の「主要耐久消費財等の普及率」「主要耐久消費財の保有数量の推移」(リンク)によると、2人以上の世帯のPC普及率は77.0%、100世帯辺り123.6台(2020年3月)だそうです。
保有世帯だけを考えれば123.6 / 0.77 / 100 = 1.61 [台/世帯] ですから、世帯人数 <PC台数です。PCを日常的に使う習慣がない限り、共有のPCが1台あれば十分ですし、納得感ある結果です。
一般のご家庭にPCは何台置ける?
では、一般のご家庭にPCは最大で何台置けるでしょうか?
PCの消費電力は様々ですが、夢はでっかく、高性能PCとして、AMD Threadripper 3990X, NVIDIA GeForce RTX 3090のマシンを考えましょう。CPUとグラボのTDPは280 + 350W = 630Wです。他の部品や損失を考えると、PC 1台あたり800W程度と思われます。
一般家庭の我が家の電気契約(40A)ですと、5台程度でブレーカーが飛びます。200V系のコンセントを増設し、200Vで給電すれば電流は半減するので10台くらいは置けるでしょう。30A契約のご家庭も多いでしょうから、「高性能PC 8〜10台」これが一般のご家庭の限界と思われます。
逸般の誤家庭にPCは何台置ける?
では、色々逸脱した逸般の誤家庭の場合はどうでしょうか?
家庭の電気契約は「従量電灯B」という契約(従量電灯B・C電気料金プラン - 東京電力エナジーパートナー株式会社)がほとんどです。従量電灯Bの最大契約アンペア数は60Aで、全て200Vから取ると最大12kWです。したがって12000 / 800 = 15台が限界です。ふーむ、意外と伸びませんね。
冷却の電力は完全に無視しています。冷却を無視したまま15台も置いたら、家の中は一瞬で灼熱地獄になり、人間もPCも死ぬと思います。
業務用なら青天井
大口需要向けに「従量電灯C」という契約もあります。
従量電灯Cの場合10Aごとに基本料金が従量的に増える青天井の契約になります。一般家庭でも契約可能のようです。基本料金を比較すると、従量電灯B< 従量電灯Cとなるため、一般のご家庭だと損するだけで契約する意味はありません。
本来、家電が大量にある豪邸や、業務用の電気機器がある商店用ですが、60Aに満足できない真の逸般の誤家庭にも向いているかもしれませんね。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年2月15日
Wikipediaの数学のページを眺める
群とか環とか体とか、大学で教えてもらった記憶がうっすらありますが、何回見ても忘れます。幸いにもWikipedia先生に割と詳しく解説されているので、まとめておこうと思います。
群
集合Gと二項演算uの組(G, u)を考えます。uは乗法や加法と呼ばれる場合があるようです。以降u(a, b) をa + bの形で表します。
- 半群
- 閉性を満たす: 二項演算u(u: G + G -> G)の結果はGに含まれる
- 結合法則を満たす: a + (b + c) = (a + b) + c
- モノイド
- 単位元eが存在する: a + e = e + a、整数の加法でいえば0
- 群
- 逆元xが存在する: a + x = x + a = e整数の加法でいえば -a
- アーベル群
- 交換法則を満たす: a + b = b + a
下にある群は、上の群の性質をすべて満たします(以降も特に断りがなければ同じ)。なので、モノイドは半群の性質を満たしますし、群はモノイドと半群の性質を満たします。
環
集合Rと2つの二項演算u, tの組(R, u, t) を考えます。(R, u) はアーベル群です。uは加法、tは乗法と呼ばれるようです。以降t(a, b) をa * bの形で表します。
- 乗法半群
- 閉性を満たす: 二項演算t(t: R * R -> R)の結果はRに含まれる
- 結合法則を満たす: a * (b * c) = (a * b) * c
- 乗法モノイド
- 単位元eが存在する: a * e = e * a、整数の乗法でいえば1
- 環(モノイドでない場合がある)
- 加法の上に左分配律を満たす: a * (b + c) = (a * b) + (a * c)
- 加法の上に右分配律を満たす: (a + b) * c = (a * c) + (b * c)
- 可換環(モノイドでない場合がある)
- 交換法則を満たす: a * b = b * a
群と違って、環はモノイド(単位元が存在する)である必要はないみたいです。
零因子
可換環では零でない零因子という困ったことが起きます。
- a * x = 0となるx != 0が存在するときaは左零因子
- y * a = 0となるy != 0が存在するときaは右零因子
困る例として挙げられていたのはa * b = 0かつa != 0でもb = 0とは限らない、もしくは、a * b = a * cかつa != 0でも、b = cとは限らない、という例でした。
具体的な例が載ってませんでしたが、行列の和と積を考えると発生しそうに思えます。
左零因子になるかな?
A = [1, 1] [0, 0] B = [ 1, 0] [-1, 0] C = [0, -1] [0, 1] A * B = [0, 0] [0, 0] A * C = [0, 0] [0, 0] A != 0だがB, Cは零行列ではない。A * B = A * Cだが、B = Cでもない。
環はこういうパターンが無数に出てきて、さらに条件を厳しくしないと困る場合がありますよ、ということですかね?
整域
変わった名前ですが、環の一種のようです。環で発生する零因子による困った問題を排除しています。
- 整域(乗法モノイドである必要がある)
- 零が唯一の零因子: a * x = 0かつa != 0ならばx = 0
- 非自明環: 自明環(零のみの集合は {0} 環となるので、自明環と呼ばれる)ではない
力尽きた
群環体の「体」まで辿り着きたかったのですが、整閉整域、一意分解整域、主イデアル整域、ユークリッド整域、体、有限体、と訳のわからない名前のオンパレードで、力尽きました。また今度調べます。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
| < | 2021 | > | ||||
| << | < | 02 | > | >> | ||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| - | 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | - | - | - | - | - | - |
こんてんつ
 wiki
wiki Linux JM
Linux JM Java API
Java API過去の日記
 2002年
2002年 2003年
2003年 2004年
2004年 2005年
2005年 2006年
2006年 2007年
2007年 2008年
2008年 2009年
2009年 2010年
2010年 2011年
2011年 2012年
2012年 2013年
2013年 2014年
2014年 2015年
2015年 2016年
2016年 2017年
2017年 2018年
2018年 2019年
2019年 2020年
2020年 2021年
2021年 2022年
2022年 2023年
2023年 2024年
2024年 2025年
2025年 2026年
2026年 過去日記について
過去日記についてその他の情報
 アクセス統計
アクセス統計 サーバ一覧
サーバ一覧 サイトの情報
サイトの情報合計:
本日:
 未来から過去へ表示(*)
未来から過去へ表示(*)