2022年1月4日
Windows電卓
Windows電卓は浮動小数点数を扱えます。10^9999から10^-9999という非常に大きい数から、小さい数まで扱えます。
単精度浮動小数点数の最小値は10^-38(正規化数)もしくは10^-45程度、倍精度浮動小数点数でも最小値は10^-308(正規化数)もしくは10^-324(非正規化数)程度ですから、IEEE 754準拠の浮動小数点数型ではなさそうです。

Windows電卓で1 - 1.e-204 - 1を計算した結果
そのためか少し変わった桁落ちの挙動を示します。同じ程度の大きさの数同士の演算(例: 1.e-9999 + 1.e-9999 = 2.e-9999)であれば桁落ちしませんが、大きい数と小さい数を演算(例: 1 - 1.e-204 - 1 = -9.807971461541689e-149)すると激しく桁落ちします。
Windows電卓はオープンソース
実はWindows 10の電卓のソースコードはGitHubに公開されていて(GitHubのプロジェクトへのリンク)、誰でも見ることができます。MITライセンスで、2019年に公開されたそうです。Windowsの標準アプリがオープンソースになっているなんて、調べるまで知りませんでした。
利用方法は簡単でGit cloneしたあと、Visual Studioでsrcディレクトリの下にあるCalculator.slnを開くだけです。私のノートPCが非力なせいか、ビルドは非常に遅いですね……。
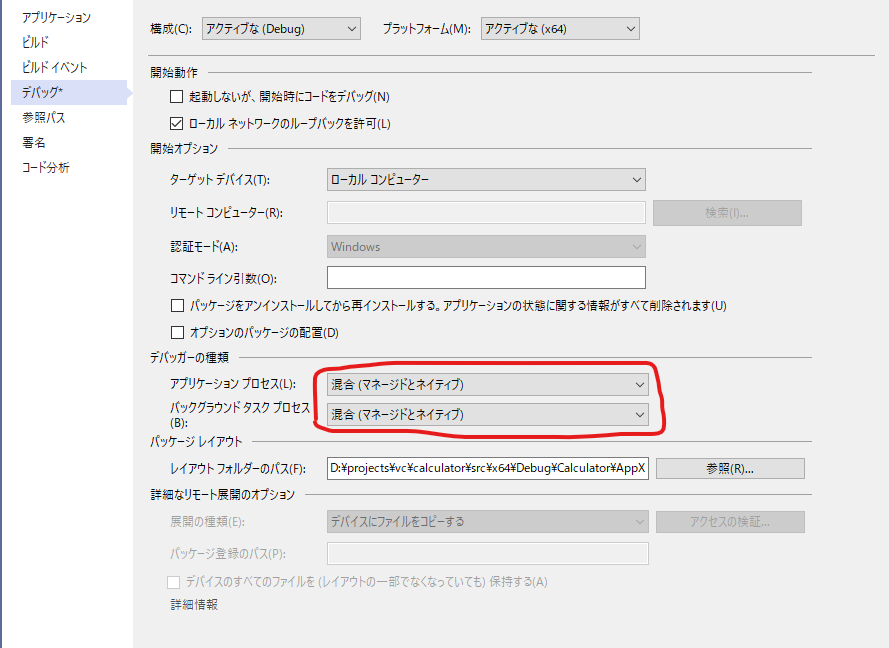
デバッグする際は、設定を「マネージド+ネイティブ」にしておかないと、ネイティブコードを実行している部分のデバッグが全くできず、ブレークポイントなどが無視されるので注意が必要です。
桁落ちしている箇所
コードのありかとデバッグ方法がわかったところで、Windows電卓のコードを調べます。桁落ちはどこで発生しているでしょうか?
先ほど示した1 - 1.e-204 - 1という演算の場合、CalcManagerプロジェクトのRatPack/rat.cppのaddrat() 関数にてtrimit() を呼んでいる箇所で桁落ちが発生します。
数値表現と加算の実装
//calculator/src/CalcManager/Ratpack/ratpak.h
typedef uint32_t MANTTYPE;
...
//-----------------------------------------------------------------------------
//
// NUMBER type is a representation of a generic sized generic radix number
//
//-----------------------------------------------------------------------------
#pragma warning(push)
#pragma warning(disable : 4200) // nonstandard extension used : zero-sized array in struct/union
typedef struct _number
{
int32_t sign; // The sign of the mantissa, +1, or -1
int32_t cdigit; // The number of digits, or what passes for digits in the
// radix being used.
int32_t exp; // The offset of digits from the radix point
// (decimal point in radix 10)
MANTTYPE mant[];
// This is actually allocated as a continuation of the
// NUMBER structure.
} NUMBER, *PNUMBER, **PPNUMBER;
#pragma warning(pop)
//-----------------------------------------------------------------------------
//
// RAT type is a representation radix on 2 NUMBER types.
// pp/pq, where pp and pq are pointers to integral NUMBER types.
//
//-----------------------------------------------------------------------------
typedef struct _rat
{
PNUMBER pp;
PNUMBER pq;
} RAT, *PRAT;
//calculator/src/CalcManager/Ratpack/rat.cpp
void addrat(_Inout_ PRAT* pa, _In_ PRAT b, int32_t precision)
{
PNUMBER bot = nullptr;
if (equnum((*pa)->pq, b->pq))
{
// Very special case, q's match.,
// make sure signs are involved in the calculation
// we have to do this since the optimization here is only
// working with the top half of the rationals.
(*pa)->pp->sign *= (*pa)->pq->sign;
(*pa)->pq->sign = 1;
b->pp->sign *= b->pq->sign;
b->pq->sign = 1;
addnum(&((*pa)->pp), b->pp, BASEX);
}
else
{
// Usual case q's aren't the same.
//★bを変更できないので見づらい書き方になっているが、通分して加算している
//★pa = pa->pp / pa->pq = A / B, b = b->pp / b->pq = C / Dとおくと
DUPNUM(bot, (*pa)->pq); //★bot = B
mulnumx(&bot, b->pq); //★bot = BD
mulnumx(&((*pa)->pp), b->pq); //★pa = AD / B
mulnumx(&((*pa)->pq), b->pp); //★pa = AD / BC
addnum(&((*pa)->pp), (*pa)->pq, BASEX); //★pa = (AD + BC) / BC
destroynum((*pa)->pq);
(*pa)->pq = bot; //★pa = (AD + BC) / BD
trimit(pa, precision); //★★この呼び出しで桁落ち★★
// Get rid of negative zeros here.
(*pa)->pp->sign *= (*pa)->pq->sign;
(*pa)->pq->sign = 1;
}
#ifdef ADDGCD
gcdrat(pa);
#endif
}
Windows電卓は内部ではRAT型(struct rat型)で数値を保持しています。RATは分子ppと分母pqの2つのNUMBER型で構成された有理数を表す型です。
有理数の加算は小学校で習った通りで、通分して足します。大きな数+小さな数で通分すると、非常に仮数部(構造体のmant、mantissa: 仮数の意味)が長くなってしまいます。例えば1 + 1.e-9999だと仮数部が9511要素もあるint32_tの配列になります。trimit() は一定以上の仮数を切り落とす役目を果たします。

加算の桁落ちを削除したWindows電卓で1 - 1.e-204 - 1を計算した結果
桁落ちを防止したければtrimit() の呼び出しを削れば良いです。しかし不思議なことに完全にtrimit() を削除するとWindows電卓が起動しなくなります。
桁落ちは必須
桁落ちを防止すると起動しなくなる理由は、Windows電卓はなぜか起動時にCCalcEngineのコンストラクタにて10^100を計算しているからです。
Windows電卓はx^yをx^y = exp(y * ln(x)) で求めているので、logの実装を見ましょう。ソースコードはexp.cppの _lograt() です。見たところ、十分に小さい項までテイラー展開を続けるアルゴリズムのようです。
logの実装
//calculator/src/CalcManager/Ratpack/exp.cpp
void _lograt(PRAT* px, int32_t precision)
{
CREATETAYLOR();
createrat(thisterm);
// sub one from x
(*px)->pq->sign *= -1;
addnum(&((*px)->pp), (*px)->pq, BASEX);
(*px)->pq->sign *= -1;
DUPRAT(pret, *px);
DUPRAT(thisterm, *px);
n2 = i32tonum(1L, BASEX);
(*px)->pp->sign *= -1;
do
{
NEXTTERM(*px, MULNUM(n2) INC(n2) DIVNUM(n2), precision);
TRIMTOP(*px, precision);
} while (!SMALL_ENOUGH_RAT(thisterm, precision));
DESTROYTAYLOR();
}
桁落ちを一切なくすとループが終わらなくなってしまいます。変数thistermが0にならないとループを抜けないところを見ると、ループ条件のSMALL_ENOUGH_RATがバグっているような気もするんですが……、これ以上の深追いはやめておきます。
他にも √ の計算も非常に遅くなります。パフォーマンスと実用性のバランスからtrimit() は必須といえるでしょう。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2022年1月3日
北海道から東京へ
オミクロン株が若干不穏な気配ですが、今年は久しぶりに北海道に帰省しました。でも次の帰省はいつになるやら……。COVID-19の動向次第ですね。
今までは帰省時期に飛行機に乗るとほぼ必ずインフルエンザをもらっていたのですが、今年は風邪一つ引きませんでした。道行く人が全員マスクを着ける、というのは本当に伝染病予防に効くんですね。マスクの効果を疑っていたわけではないですけど、思った以上の効果が出ていて驚いています。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年12月28日
ゲーム - まとめリンク
目次: ゲーム
- Nintendo DSを買った
- パネルでポンDS
- 最近の朝はパネポンDS
- 聖剣伝説DSチルドレン・オブ・マナをクリア
- シムシティDS2クリア
- PlayStation Vitaのアプリ達が寿命を迎えている
- Wizardry(囚われし亡霊の街)敵が強すぎる
- ポケモンGO
- MAD Tower Tycoon楽しい
- MAD Tower Tycoonコンプリート
- The Hunter: Call of the Wild
- PlayStation Vitaのアプリがめちゃ減っている
- ファイアーエムブレム 風花雪月
- ぶきあつめコンプリート
- ノートPCでゲームは辛いよ
- ゲーム用のPCを作りたいが、高い
- DUNGEON ENCOUNTERSクリア
- DUNGEON ENCOUNTERS完全踏破
- ゲーム用PCを作ろう
- ドラクエ1の「ド」
- shapezレベル100達成
- 首都高バトルSteam版
- 首都高バトルSteam版、大体クリア
- 首都高バトルSteam版、伝説のチューナー
- 首都高バトルSteam版、フルチューン後の姿 - その1
- 首都高バトルSteam版、フルチューン後の姿 - その2
- 首都高バトルSteam版、フルチューン後の姿 - その3
- Nintendo Switch 2当選
- 歴代据え置きハードのCPUとGPU
- タローマンのゲームTAS動画
鉄道シミュレーションゲーム、Transport Fever 2の話です。
- Transport Fever 2楽しい
- Transport Fever 2ひと段落
- Transport Fever 2大都市達成のヒント
- Transport Fever 2初めの一歩 - その1
- Transport Fever 2初めの一歩 - その2
- Transport Fever 2初めの一歩 - その3
駅シミュレーションゲーム、STATIONflowの話です。
- STATIONflow始めました、超えろ、新宿駅
- STATIONflowランク20
- STATIONflowのバグ
- STATIONflow小技
- STATIONflowプレイ日記
- STATIONflowまさかの実績解除方法
- STATIONflowの駅の評価
- STATIONflowランク100
- STATIONflow実績コンプリート
ゲームプラットフォーム、Steamの話です。
目次: 一覧の一覧
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年12月27日
DUNGEON ENCOUNTERS完全踏破
目次: ゲーム
ダンジョンエンカウンターズ、全フロアを踏破しました。基本的には強敵を避けてウロウロ歩けば踏破できますし、アビリティ「ノーエンカウント」取得後は、落とし穴以外に恐れるものは存在せず、ほぼ塗り絵ゲームになります。ただし、地下92階だけはかなり辛いです……。
魔の地下92階
おそらく全員が「最も踏破に苦労する階は?」という質問に対して「地下92階」と答えるでしょう。それくらい面倒くさい作りです。地下92階は全て飛び地になっていて、一部は地下93階から02(上り階段)で行けますが、残りはほとんど目印がありません。マップの背景(宇宙みたいな赤と青のモヤモヤ)から、飛び地の座標に当たりを付け、アビリティ「仮想階段上り」で上る必要があります。
地下92階から「仮想階段下り」で地下93階に戻ると、いきなり落とし穴に落ちることがありますが、地下94階で必ず受け止めてくれるので心配いりません。
しかし落ちた先の地下94階や、地下92階の小島でミスって落とし穴を踏むと「奈落の底に落ちてパーティーが全員行方不明」になることがあります。被害を最小限にするためにも、地下92階は1人パーティーで攻略した方が良いと思います。入り口となる地下93階は常に一本道です。落とし穴回避のためアビリティ「ムーブ」「ナイトムーブ」、エンカウントマスも回避できないため「ノーエンカウント」もほぼ必須でしょう。
全部巡るのは非常に大変でしたが、下記の表で座標を全部メモできているはずです。
| 島の種類 | 南 | 東 | 島の広さ |
|---|---|---|---|
| 02階段上り | 2 | 41 | 16 |
| 02階段上り | 14 | 72 | 20 |
| 02階段上り | 15 | 13 | 4 |
| 02階段上り | 21 | 34 | 16 |
| 02階段上り | 33 | 87 | 16 |
| 02階段上り | 36 | 20 | 12 |
| 02階段上り | 47 | 34 | 16 |
| 02階段上り | 49 | 83 | 16 |
| 02階段上り | 61 | 10 | 20 |
| 02階段上り | 72 | 43 | 16 |
| 02階段上り | 73 | 83 | 16 |
| 02階段上り | 74 | 15 | 20 |
| 02階段上り | 92 | 41 | 16 |
| 02階段上り | 94 | 88 | 9 |
| Event 3Fの島 | 49 | 60 | 25 |
| Event FDの島 | 87 | 14 | 9 |
| 仮想階段上り | 5 | 54 | 20 |
| 仮想階段上り | 9 | 73 | 4 |
| 仮想階段上り | 10 | 83 | 12 |
| 仮想階段上り | 10 | 19 | 16 |
| 仮想階段上り | 14 | 54 | 16 |
| 仮想階段上り | 16 | 30 | 12 |
| 仮想階段上り | 17 | 81 | 20 |
| 仮想階段上り | 18 | 26 | 12 |
| 仮想階段上り | 19 | 39 | 12 |
| 仮想階段上り | 19 | 63 | 12 |
| 仮想階段上り | 24 | 45 | 16 |
| 仮想階段上り | 25 | 20 | 20 |
| 仮想階段上り | 27 | 58 | 12 |
| 仮想階段上り | 27 | 75 | 20 |
| 仮想階段上り | 29 | 6 | 15 |
| 仮想階段上り | 30 | 29 | 16 |
| 仮想階段上り | 37 | 65 | 12 |
| 仮想階段上り | 39 | 42 | 9 |
| 仮想階段上り | 40 | 50 | 20 |
| 仮想階段上り | 41 | 99 | 15 |
| 仮想階段上り | 41 | 79 | 20 |
| 仮想階段上り | 52 | 37 | 4 |
| 仮想階段上り | 55 | 20 | 20 |
| 仮想階段上り | 58 | 48 | 16 |
| 仮想階段上り | 61 | 94 | 16 |
| 仮想階段上り | 63 | 0 | 12 |
| 仮想階段上り | 67 | 19 | 20 |
| 仮想階段上り | 68 | 32 | 6 |
| 仮想階段上り | 68 | 77 | 16 |
| 仮想階段上り | 70 | 92 | 9 |
| 仮想階段上り | 71 | 65 | 16 |
| 仮想階段上り | 77 | 50 | 9 |
| 仮想階段上り | 79 | 80 | 16 |
| 仮想階段上り | 80 | 27 | 20 |
| 仮想階段上り | 83 | 39 | 6 |
| 仮想階段上り | 87 | 59 | 20 |
| 仮想階段上り | 89 | 68 | 16 |
| 仮想階段上り | 95 | 25 | 20 |
サイトだと見づらいと思うので、Googleスプレッドシートにも置きました(Googleスプレッドシートへのリンク)。基本的には地下93階の「曲がり角」で仮想階段を使う座標にしたはずです。間違ってたらゴメンなさい&コメントなどで教えてくれると嬉しいです。
攻略の途中で「この地下92階は山勘でやってもクリア不可能じゃね?」と感じてメモを始めたため、踏破済みと未踏破が中途半端に混ざった状態からメモを始めることになりました。おかげで島の座標を全部列挙したかどうかの検証がめちゃくちゃ面倒くさかったです……。最初からメモすれば良かったよー。
真のラスボスは諦めた
「無限」より強いと思われるのが、バトルFDの「モルモット教授」という敵です。出会える確率が非常に低い、防御とHPが9,999,999の最強タフネス、驚異のスピード130、数ターン耐えるのが限界の超強力な攻撃、と嫌な点の塊のような敵です。
幸い?なことにアイテムを何もドロップしませんから、倒す必要がありません。無視してOKです。ただただやり込みプレイを阻むためだけに用意された、嫌がらせのような敵です。
私もアドレスブレイド3本とスピード重視装備で挑んでみましたけど、防御すら削りきれないうちに瞬殺されて心が折れました……。勝てる気がしません。もういいわ。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年12月26日
DUNGEON ENCOUNTERSクリア
目次: ゲーム
ダンジョンエンカウンターズ、やっと最後まで行きました。謎解きはまじめにやらず、攻略サイトを見てしまいました。難しいというか……正解を見ても「無茶言うなよ」って感じの問題です。攻略サイト作っている人たちはどうやって解いたんでしょうね……?
ラスボス1
地下90階にいるラスボスを倒して1回目のスタッフロールを拝むのはそんなに難しくありません。とはいえ、強いのは確かです。特に2回目の戦闘(パノプティコアA, B, C, D)は、何も考えずに突っ込むとパーティーが蒸発します。ラスボスを無視して、地下99階までの謎解きアイテムとアビリティを全部拾ってから改めて挑むと比較的楽だと思います。アビリティ「テレポ」と「ノーエンカウント」を拾うと回収が捗ります。
- 武器: アドレスブレイド(単体物理、アドレス依存ダメージ)
- 武器: ジャベリン(全体物理375,000)
- 武器: トウルヌソル(単体物理100,000)
- アビリティ: 防御系全部、HP満タン攻撃力倍、精神統一(飛行に剣や槍が当たる)
謎解きを済ませると、この辺の超強力な武器が全て揃うはずです。地下90階以降の敵はアホみたいに攻撃力が高く、一撃で防御値がなくなることが多いため、防具を1〜2段階強化してもほぼ意味がありません。スピードの落ちる重装備(ヘルム、鎧)より、スピード重視で軽装備(服、帽子)+ブーツにして、相手より早く殴って倒すようにすると良いでしょう。
- ブーツ: コスト内で速度が一番上がるもの
- 防具: コスト内で速度の落ちない軽装備、ただし裸は即死するのでNG
パノプティコアは1体だけ残すと「全ての力」という超強烈な攻撃をしてきて、メンバーが一瞬で蒸発するので、
- HPが低いAを速攻で潰す
- スピードの速いDをアドレスブレイドで殴りまくって潰す
- 残ったノロマのBとC 2体をアドレスブレイドで殴り、HPはトウルヌソルで削る
- 最後にジャベリンで2体同時に倒す
こうすると比較的楽なはずです。
ラスボス2
最下層の地下99階にいるバトルFF「無限」というクッソ強い敵を倒すと2回目のエンディングが拝めます。拾える武器だけでもうまくやれば倒せる気がするんですけど、私はやり方がうまくないのか、火力不足で勝てませんでした。
地下98階辺りの、バトルF7を集中的に選んで、ティアマットLv.99が落とすアドレスブレイドを2本を拾うまで頑張ります。出てくる敵としては、
- ティアマットLv.99
- メインターゲットです。スピード80で比較的行動が早いうえ、ほぼ確実に全体物理攻撃(咆哮: 割合ダメージなので雑魚、なぎ倒す: 超強烈で物理防御が一撃でなくなる)をしてきて超危険です。幽霊船の番が来ないなら、こいつを集中攻撃で潰しましょう。
- 幽霊船Lv.99
- スピード85、飛行状態、高確率で全体物理攻撃(砲撃: 強烈な物理攻撃、恐怖: 確率で物理防御破壊)をしてくる危険な相手です。ですが幸いなことにHP 1なので、「精神統一」アビリティ、全員を「物理武器+素手」にしておけば、素手パンチをお見舞いして確実に倒せます。ホクガクの刀攻撃も有効です。
- ウィールワーターLv.98
- 単体、全体魔法攻撃を使ってきますが、全体攻撃は半々くらいですかね。スピード65と遅く、攻撃頻度は低いです。先行で魔法攻撃を食らって魔法防御がなくなったとしても、次の攻撃を食らう前に、ジャベリンとアドレスブレイドの順が回ってきて確実になぎ倒せるはずです。
バトルF8の方がティアマットが確実に出ますが、一気に5体出てきて強力な全体物理攻撃を連発され、パーティーが一瞬で全滅する可能性が高く、面倒な相手です。バトルF7を数こなす方が安定すると思います。
アドレスブレイドを揃えたら、地下99階のなるべく南東のマスに「無限」を出現させます。装備はHP満タン攻撃力倍+スピード重視装備+アドレスブレイドで。アドレスブレイド持ちのキャラはとにかく殴り、防御が完全に剥がれたキャラやアドレスブレイドを持っていないキャラは防御回復を連打、これでたぶん倒せるはずです。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年12月24日
サンタがマッハ2で街にやってくる(2021年)
目次: サンタ
飛行機の位置をリアルタイムに表示するFlightradar24というサービス(サイトへのリンク)があります。飛行機やヘリコプターが発するADS-Bという信号を、世界中の有志が受信して、Flightradar24のサーバーに送ることで実現しているそうです。へえ〜。
仕組みはさておいて、このサービスではクリスマス・イブの日にはサンタが出現する毎年恒例のお約束演出があります。夜にサンタの飛んでいる様をボーっと眺めていました。
マレーシア上空をインド方面に飛んでいましたが、どうも移動速度が速いような気がしてなりません。表示上は40ノット(時速74.8km/h)となっています。しかしマレーシアをあっさりと横断して、インド洋に抜けており、そんなゆっくり飛んでいるように見えません。
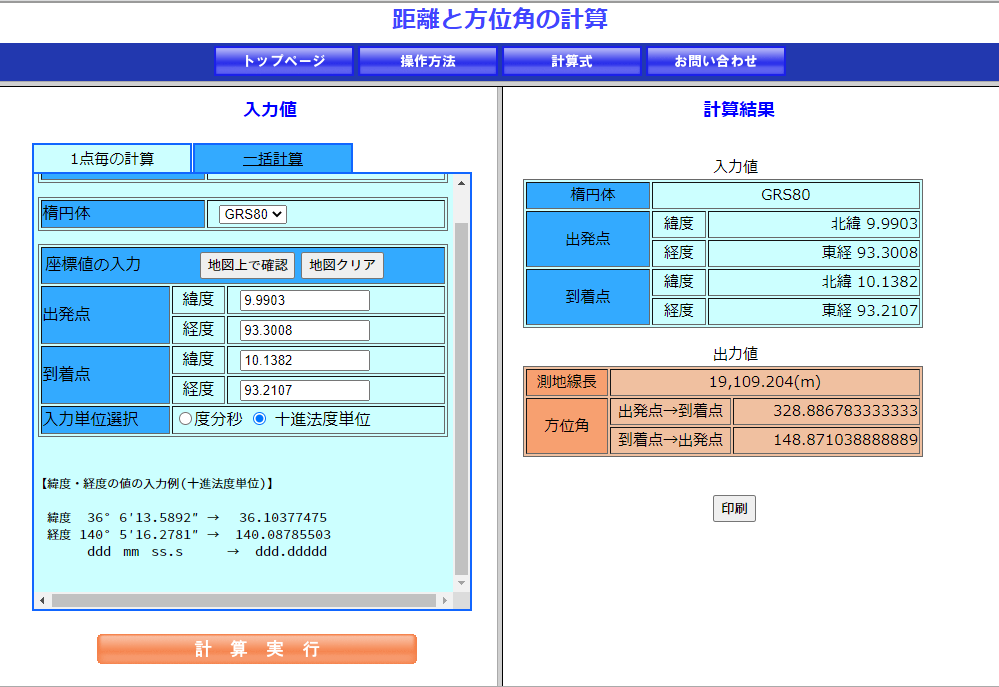
サンタの対地速度
サイトの速度表示は無視して、2地点間の距離で速度を測ってみました。
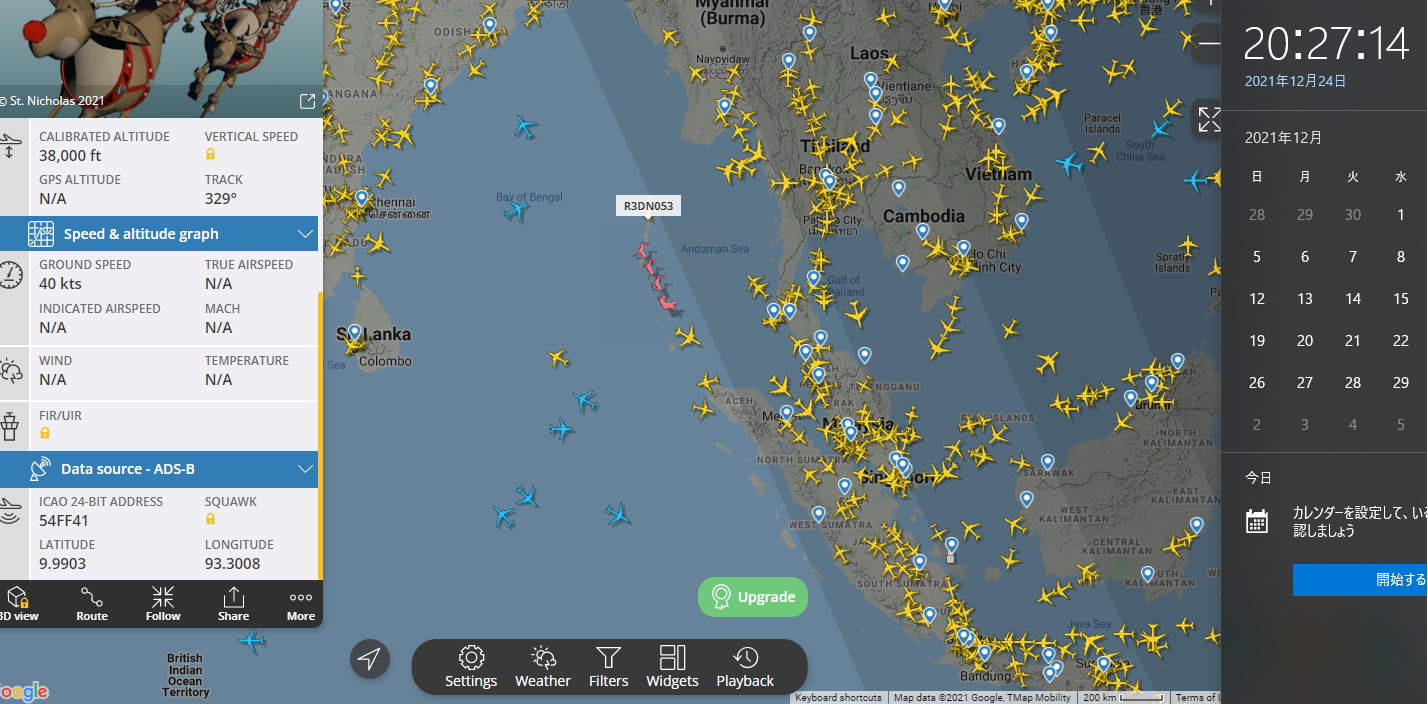
20:27:14時点の位置(緯度9.99903度、経度93.3008度)
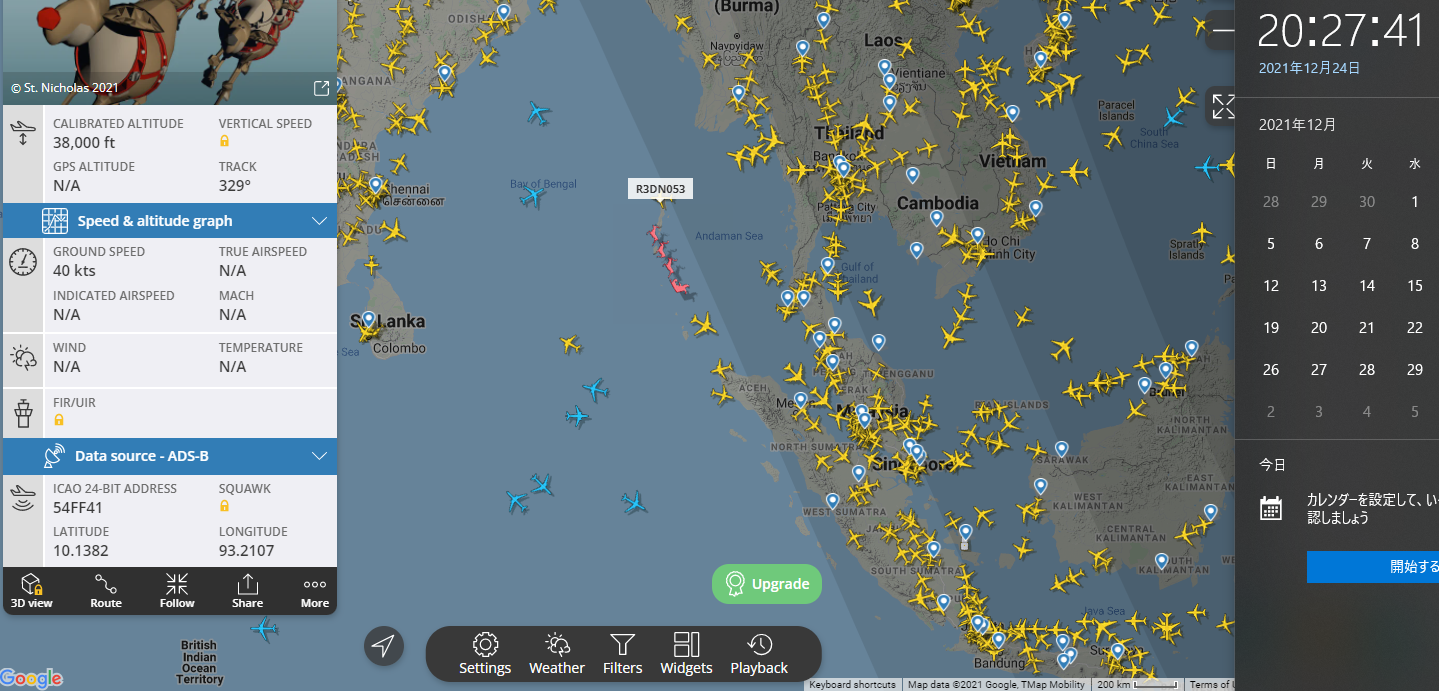
20:27:41時点の位置(緯度10.1382度、経度93.2107度)
緯度、経度から距離を出すときは、地球の形状(赤道方向がやや長い、楕円形)を考慮したりで割と面倒らしいんですが、国土地理院のページを使うと一発で計算してくれて超便利です(サイトへのリンク)。
2地点間の距離は約19.1kmで、時間差は27秒なので、対地速度は約2,546km/hです。地上で言うところのマッハ2くらい(ただし、上空34,000ftsだとマッハ数はもっと高く出る)です。旅客ジェット機は対地速度800km/hくらい(マッハ 〜0.8程度)なので、ジェット機の2〜3倍速です。
戦闘機の巡航速度がマッハ1くらいで、アフターバーナーでマッハ2超えるくらいらしいので、サンタさんめっちゃ速いやん……。戦闘機とやりあう気かよ??
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
2021年12月23日
GL10PのSIMロック解除(思い出)
懐かしい画面キャプチャが出てきたので供養しておきます。
だいぶ昔になりますが、イーモバイルのWiFiルーターHuawei GL10Pを買いました。イーモバイルの契約は5年前(2016年11月27日の日記参照)に解約してしまったので、GL10Pだけが寂しく残っている状態でした。
といってもモバイルWiFiルーターはほとんど使わないので、イーモバイル(今はワイモバイルでしたっけ?)を再契約するほどでもありません。
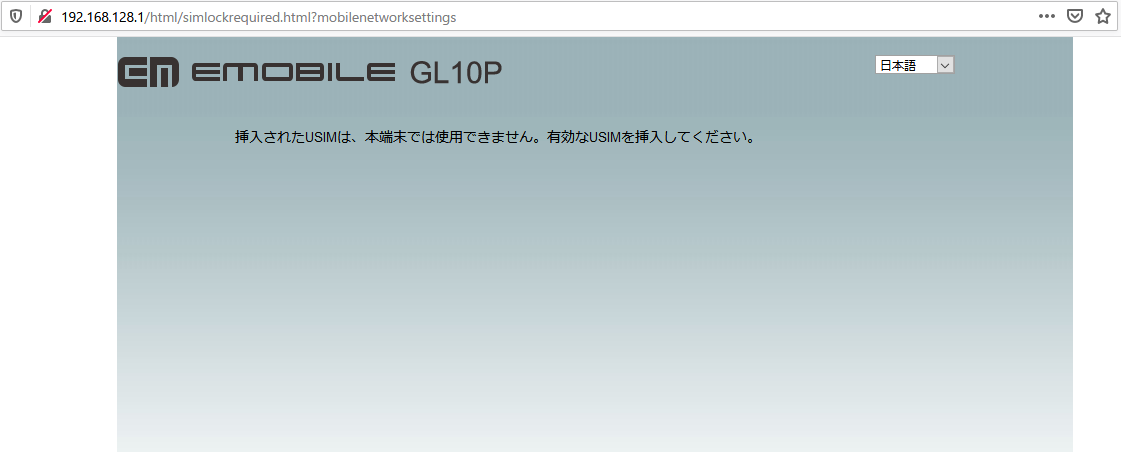
とりあえず何か通信さえできれば良いので、今はb-mobileの格安SIM(ドコモ回線)を入れています。ただしこの時代のイーモバイルのWiFiルーターはSIMロックが掛かっているので、SIMロックを解除する必要があります。SIMロック解除には解除コードが必要(コードを知る方法はググると出てきます)です。以降、コードは既にわかっているものとします。
GL10PにWiFiで接続して、パスワードadminでログインします。おそらく下記のような画面が出ているはずです。
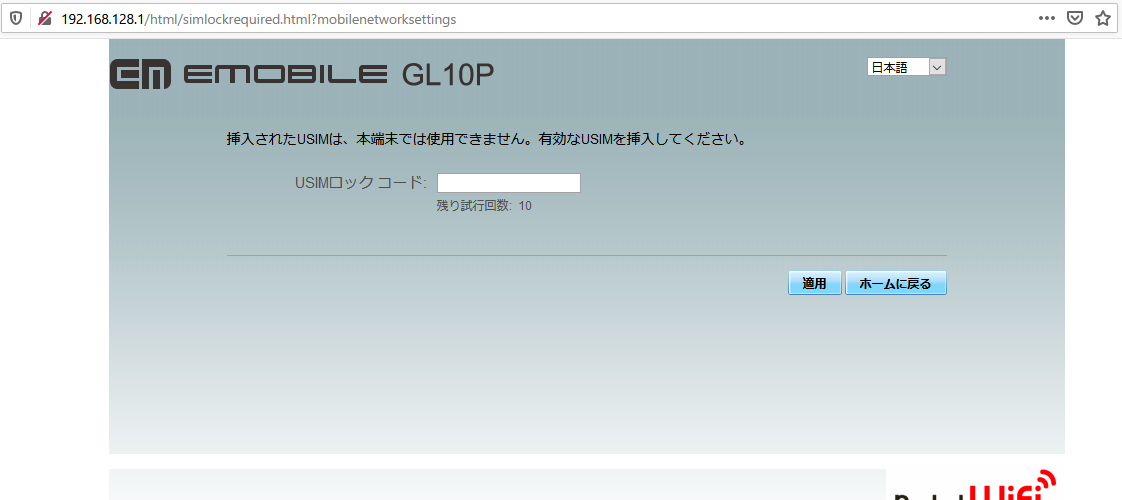
このページにはSIMロック解除コードが隠れているので、DOMインスペクタなどで入力欄を表示させます。
追加のツール等は不要な親切設計となっていて、ありがたい限りです。Huaweiが意図して提供した機能か、デバッグ用の機能が紛れ込んだのか、どちらなのか知りませんけども……。
コメント一覧
- コメントはありません。
 この記事にコメントする
この記事にコメントする
| < | 2022 | > | ||||
| << | < | 01 | > | >> | ||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| - | - | - | - | - | - | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | - | - | - | - | - |
こんてんつ
 wiki
wiki Linux JM
Linux JM Java API
Java API過去の日記
 2002年
2002年 2003年
2003年 2004年
2004年 2005年
2005年 2006年
2006年 2007年
2007年 2008年
2008年 2009年
2009年 2010年
2010年 2011年
2011年 2012年
2012年 2013年
2013年 2014年
2014年 2015年
2015年 2016年
2016年 2017年
2017年 2018年
2018年 2019年
2019年 2020年
2020年 2021年
2021年 2022年
2022年 2023年
2023年 2024年
2024年 2025年
2025年 2026年
2026年 過去日記について
過去日記についてその他の情報
 アクセス統計
アクセス統計 サーバ一覧
サーバ一覧 サイトの情報
サイトの情報合計:
本日:
 未来から過去へ表示(*)
未来から過去へ表示(*)